La rigidez torsional explica la capacidad de una estructura para soportar la fuerza de torsión. Componentes como puentes, rascacielos y engranajes están diseñados para resistir la fuerza o la carga para funcionar eficazmente. Sin esto, podría haber algunos efectos secundarios adversos.
En esta guía, le explicamos lo que necesita saber sobre la rigidez torsional, incluidas sus aplicaciones, etc.
¿Qué es la rigidez torsional?
La rigidez torsional es la capacidad de un material o estructura para resistir la torsión cuando se aplica una fuerza de torsión. Mide la capacidad de un componente para resistir la deformación cuando actúa sobre él una fuerza de torsión.
La rigidez torsional es importante en ingeniería estructural porque explica hasta qué punto un objeto, una pieza o un material puede soportar una determinada carga sin perder su resistencia, forma o daños.
Propiedades y fórmulas clave
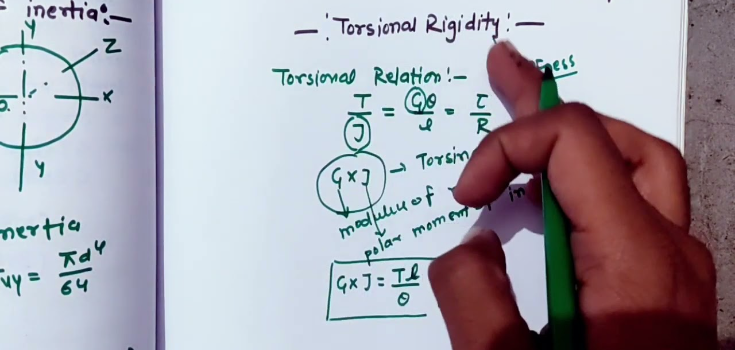
La rigidez torsional se representa como GJ, indicando G el módulo de cizalladura, mientras que J es el momento polar de inercia.
También se puede obtener el valor de la rigidez a la torsión a partir de la fuerza aplicada y el ángulo de torsión. La unidad de medida de la rigidez a la torsión es Nm².
Ecuación de rigidez torsional: GJ = TL/θ o θ = TL/JG
Dónde,
J = Momento polar de inercia
G= Módulo de cizallamiento
T = Par aplicado
L = Longitud del objeto
θ = Ángulo de torsión
Módulo de cizallamiento
El módulo de cizalladura es la capacidad de un componente para soportar un esfuerzo de cizalladura o una deformación. Se considera como la relación entre la tensión y la deformación. Si un material tiene un valor más alto de relación tensión-deformación, entonces es más probable que tenga una mayor rigidez torsional.
Momento polar de inercia
El momento polar de inercia mide la capacidad de un objeto para resistir la torsión alrededor de su eje de rotación. Factores como la forma, la composición, la masa y el tamaño influyen en el valor de esta propiedad.
Por ejemplo, es más fácil torcer caucho que metal porque el caucho tiene una masa y una composición menores. Por tanto, podemos decir que cuanto mayor es el momento polar de inercia de un material, mejor es su rigidez torsional.
Propiedades de los materiales que afectan a la rigidez torsional

El módulo de cizalladura de un material afecta a su capacidad para soportar la fuerza de torsión. El acero con un módulo de cizallamiento más alto tiene un mejor nivel de rigidez a la torsión que los polímeros o aluminio con un valor de módulo de cizallamiento inferior.
Otra propiedad del material que afecta a la rigidez a la torsión es si el material es isótropo o anisótropo.
Mientras que los materiales isótropos mantienen el mismo nivel de rigidez a la torsión independientemente de la dirección del par, el nivel de rigidez de los materiales anisótropos puede cambiar si la fuerza de torsión se aplica desde una posición diferente.
| Contenido de relleno(wt%) | Cristalinidad de la matriz(%) | G*(MPa) | σy(MPa) ±0,5 MPa |
εr(%) ±(80%) |
|
| PE | 0 | 52 | 2.8 | 16 | 1100 |
| PE-Calcita | 9.6 | 48 | 3.2 | 16 | 720 |
| PE-Calcita-SA | 7.7 | 48 | 3.1 | 15 | 720 |
| PE-Aragonito | 10.3 | 51 | 3.45 | 15 | 910 |
| PE-Aragonito-SA | 9.3 | 53 | 2.6 | 16 | 930 |
| PE-C.Fornicata | 8.6 | 49 | 2.8 | 16 | 670 |
| PE-C.Fornicata-SA | 9.5 | 49 | 3 | 15 | 740 |
| PE-C.Gigas | 6.5 | 52 | 2.8 | 16 | 730 |
| PE-C.Gigas-SA | 9.3 | 50 | 3.2 | 15 | 830 |
| PE-P.Maximus | 10.8 | 47 | 3 | 16 | 680 |
| PE-P.Maximus-SA | 9.7 | 50 | 3.2 | 16 | 760 |
Tabla comparativa del límite elástico, la resistencia a la tracción y el módulo de Young de distintos materiales
| Material | Límite elástico (MPa) |
UTS(MPa) | Módulo de Young(GPa) |
| Aluminio | 35 | 90 | 69 |
| Cobre | 69 | 200 | 117 |
| Latón | 75 | 300 | 120 |
| Hierro | 130 | 262 | 170 |
| Níquel | 138 | 480 | 210 |
| Acero | 180 | 380 | 200 |
| Titanio | 450 | 520 | 110 |
| Molibdeno | 565 | 655 | 330 |
| Aleación de circonio (revestimiento típico) | 380 | 510 | 99 |
| 08Kh18N10T acero inoxidable | 216 | 530 | 196 |
| Aleación de acero inoxidable 304L | 241 | 586 | 193 |
| SA-508 Gr.3 Cl.2(acero ferrítico de baja aleación) | 500 | 700 | 210 |
| 15Kh2NMFA(acero ferrítico de baja aleación) | 490 | 610 | 220 |
Rigidez a la torsión en diferentes formas geométricas
La forma geométrica de un objeto o material también contribuye a su rigidez torsional.
Secciones circulares
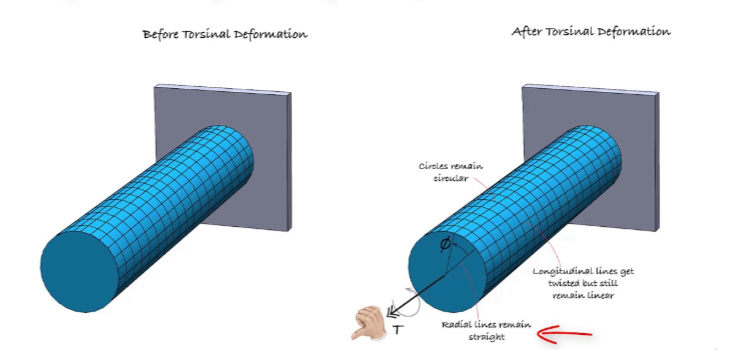
El material metálico circular resistirá la torsión a un alto nivel porque el material se distribuye uniformemente desde su centro o eje de rotación, lo que lo hace más rígido a la torsión.
Secciones transversales rectangulares
Las secciones transversales rectangulares resisten la torsión, pero no tanto como las circulares. Esto se debe a que los materiales no están distribuidos uniformemente, y los lados no contribuyen mucho a la rigidez del soporte.
Secciones transversales huecas y complejas
Las secciones huecas, como tubos y tuberías, también soportan fuerzas de torsión elevadas, ya que la parte exterior del material trabaja para resistir la fuerza y, al mismo tiempo, mantener poco peso. Se utilizan habitualmente en andamios, vigas y ejes de transmisión.
Rigidez a la torsión en distintos materiales
Por lo general, los metales con un módulo de cizallamiento elevado resisten mejor la torsión que la mayoría de los polímeros o materiales compuestos, lo que los hace adecuados para aplicaciones que requieren una gran rigidez a la torsión.
PolímerosEn cambio, tienen un módulo de cizallamiento y una rigidez torsional bajos. Sin embargo, también resultan útiles en algunas operaciones, como el acoplamiento flexible, en las que se necesita cierto nivel de flexibilidad o deformación.
Tabla comparativa de metales, polímeros y compuestos
| Tipo de material | Ejemplo de material | Módulo de cizallamiento (G) en GPa | Momento polar de inercia (J)( ×10-6m4 | Rigidez torsional (GJ) En Nm2 | Densidad relativa (kg/m³) | Aplicaciones comunes |
| Metal | Acero (AISI 1045) | 80 | 5 | 400 | 7050 | Vigas de ejes de transmisión en puentes, engranajes y ejes de máquinas. |
| Metal | Aluminio (6061-T6) | 26 | 4 | 104 | 2700 | Estructuras de aviones, cuadros de bicicletas, ruedas de automóviles y brazos. |
| Polímero | Polietileno (HDPE) | 0.8 | 3 | 2.4 | 950 | Tuberías, acoplamientos flexibles, depósitos, contenedores de plástico. |
| Polímero | Policarbonato (PC) | 2.3 | 3.5 | 8.05 | 1200 | Equipos de seguridad y cascos, carcasas de aparatos, acristalamiento de automóviles |
| Compuesto | CFRP | 100 | 6 | 600 | 1600 | Componentes aeroespaciales, automóviles de altas prestaciones y equipamiento deportivo |
| Compuesto | CFRP | 25 | 4.5 | 112.5 | 1850 | Componentes marinos, paneles de automoción |
Cómo mejorar la rigidez torsional de un material
Puedes mejorar la rigidez torsional de un material haciendo lo siguiente:
Selección del material adecuado
Cuanto mayor es el módulo de cizallamiento de un material, mayor es su rigidez torsional. El acero, por ejemplo, tiene un módulo de cizallamiento de 80GPa, lo que lo hace adecuado para operaciones que requieren una gran rigidez torsional.
Sin embargo, los polímeros tienen un módulo de cizallamiento bajo, de entre 0,5 y 3 GPa, por lo que no pueden utilizarse cuando se requiere rigidez torsional.
Aumentar el tamaño del objeto
Dado que las sustancias muy densas resisten más fuerzas de torsión que las de baja densidad, se puede mejorar la rigidez torsional del objeto aumentando su tamaño. De este modo, el objeto se vuelve más denso, lo que aumenta su capacidad para resistir fuerzas de torsión.
Mejorar el proceso de producción
Anisótropo Se sabe que los materiales tienen diferentes niveles de rigidez a la torsión en función de la dirección de la fuerza de torsión. Si se mantiene la uniformidad del material durante la producción y se utilizan materiales isótropos, se puede mejorar el nivel de rigidez a la torsión.
Aplicaciones de la rigidez torsional en ingeniería estructural

A continuación se indican algunas de las aplicaciones de la rigidez torsional en ingeniería estructural:
Rascacielos y puentes
Con la aplicación de la rigidez torsional, los ingenieros pueden diseñar puentes y rascacielos capaces de soportar altos niveles de fuerza y cargas.
Pueden determinar y construir estructuras que resistan fuerzas naturales como los terremotos. Para evitar situaciones como el derrumbe de puentes o edificios, se aseguran de que cada material estructural creado se ajuste al nivel de rigidez requerido.
Vigas y pilares
Las vigas y los pilares también deben crearse para soportar cualquier fuerza o carga de torsión. Por lo tanto, se diseñan para soportar componentes estructurales, como cubiertas, techos, voladizos, etc., para evitar que se retuerzan a causa de las cargas, el viento o los terremotos.
Rigidez torsional en ingeniería mecánica
En ingeniería mecánica, la rigidez torsional es vital, ya que explica por qué varias piezas de máquinas, incluidos ejes y engranajes, mantienen cierto nivel de rigidez cuando se someten a una fuerza de torsión.
Por ejemplo, un eje sólo se dobla mínimamente bajo torsión para que la herramienta pueda funcionar con precisión. Con ello se evitan condiciones mecánicas adversas, pero se mejora el rendimiento.
Además, el funcionamiento de los engranajes depende en gran medida de la rigidez torsional, ya que ayuda a erradicar los derrames al tiempo que garantiza que la potencia se transmita con precisión entre ellos.
Del mismo modo, en la industria automovilística y aeroespacial, la rigidez torsional contribuye a garantizar la seguridad y mejorar el rendimiento de las piezas de automóviles y aviones.
Conclusión
Para garantizar la funcionalidad, eficacia y rendimiento adecuados de los componentes o sistemas, debe asegurarse de que el material mide el nivel exacto de rigidez torsional.
DEK atiende todas sus necesidades de materiales, garantizando que cumplan el nivel de rigidez a la torsión requerido para su proyecto. Tanto si necesita orientación para la selección de su material metálico como si desea adquirirlo, siempre estamos dispuestos a hablar con usted. No dude en ponerse en contacto con nosotros.
