A rigidez torcional explica a capacidade de uma estrutura para suportar a força de torção. Componentes como pontes, arranha-céus e engrenagens são concebidos para resistir à força ou à carga para funcionarem eficazmente. Sem isso, podem ocorrer alguns efeitos secundários adversos.
Neste guia, explicamos-lhe o que precisa de saber sobre a rigidez de torção, incluindo as suas aplicações, etc.
O que é a rigidez de torção?
A rigidez de torção é a capacidade de um material ou estrutura resistir à torção quando é aplicado um binário ou uma força de torção. Mede a capacidade de um componente para resistir à deformação quando uma força de torção actua sobre ele.
A rigidez de torção é importante na engenharia estrutural porque explica até que ponto um objeto, uma peça ou um material pode acomodar uma determinada quantidade de carga sem perder a sua resistência, forma ou danos.
Principais propriedades e fórmulas
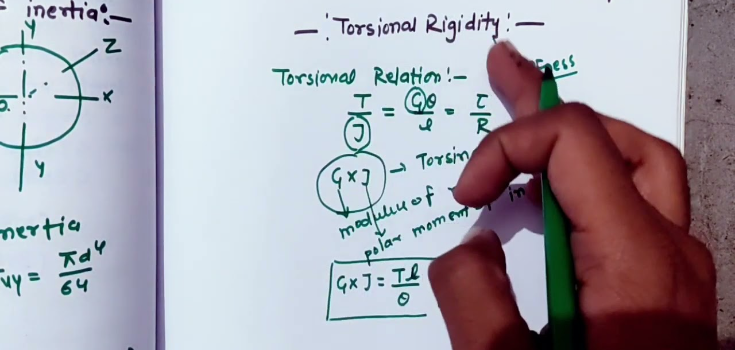
A rigidez de torção é representada por GJ, sendo G o módulo de cisalhamento e J o momento de inércia polar.
Também é possível obter o valor da rigidez de torção a partir da força aplicada e do ângulo de torção. A unidade de medida da rigidez de torção é Nm².
Equação da rigidez à torção: GJ = TL/θ ou θ = TL/JG
Onde,
J = Momento de inércia polar
G= Módulo de cisalhamento
T =Binário aplicado
L = Comprimento do objeto
θ = Ângulo de torção
Módulo de cisalhamento
O módulo de cisalhamento é a capacidade de um componente suportar tensão de cisalhamento ou deformação. É visto como a relação entre a tensão e a deformação. Se um material tiver um valor mais elevado do rácio tensão-deformação, é mais provável que tenha uma maior rigidez de torção.
Momento de inércia polar
O momento polar de inércia mede a capacidade de um objeto suportar a torção em torno do seu eixo de rotação. Factores como a forma, a composição, a massa e o tamanho influenciam o valor desta propriedade.
Por exemplo, é mais fácil torcer borracha do que metal porque a borracha tem uma massa e uma composição mais baixas. Assim, podemos dizer que quanto maior for o momento polar de inércia de um material, melhor será a sua rigidez torsional.
Propriedades dos materiais que afectam a rigidez de torção

O módulo de cisalhamento de um material afecta a sua capacidade de suportar a força de torção. O aço com um módulo de cisalhamento mais elevado tem um melhor nível de rigidez à torção do que os polímeros ou alumínio com um valor inferior de módulo de cisalhamento.
Outra propriedade do material que afecta a rigidez de torção é o facto de o material ser isotrópico ou anisotrópico.
Enquanto os materiais isotrópicos mantêm o mesmo nível de rigidez à torção independentemente da direção do binário, o nível de rigidez dos materiais anisotrópicos pode mudar se a força de torção for aplicada a partir de uma posição diferente.
| Teor de enchimento (wt%) | Cristalinidade da matriz (%) | G*(MPa) | σy(MPa) ±0,5 MPa |
εr(%) ±(80%) |
|
| PE | 0 | 52 | 2.8 | 16 | 1100 |
| PE-Calcite | 9.6 | 48 | 3.2 | 16 | 720 |
| PE-Calcite-SA | 7.7 | 48 | 3.1 | 15 | 720 |
| PE-Aragonite | 10.3 | 51 | 3.45 | 15 | 910 |
| PE-Aragonite-SA | 9.3 | 53 | 2.6 | 16 | 930 |
| PE-C.Fornicata | 8.6 | 49 | 2.8 | 16 | 670 |
| PE-C.Fornicata-SA | 9.5 | 49 | 3 | 15 | 740 |
| PE-C.Gigas | 6.5 | 52 | 2.8 | 16 | 730 |
| PE-C.Gigas-SA | 9.3 | 50 | 3.2 | 15 | 830 |
| PE-P.Maximus | 10.8 | 47 | 3 | 16 | 680 |
| PE-P.Maximus-SA | 9.7 | 50 | 3.2 | 16 | 760 |
Tabela de comparação da resistência ao escoamento, resistência à tração final e módulo de Young para diferentes materiais
| Material | Resistência ao escoamento (MPa) |
UTS(MPa) | Módulo de Young (GPa) |
| Alumínio | 35 | 90 | 69 |
| Cobre | 69 | 200 | 117 |
| Latão | 75 | 300 | 120 |
| Ferro | 130 | 262 | 170 |
| Níquel | 138 | 480 | 210 |
| Aço | 180 | 380 | 200 |
| Titânio | 450 | 520 | 110 |
| Molibdénio | 565 | 655 | 330 |
| Liga de zircónio (revestimento típico) | 380 | 510 | 99 |
| 08Kh18N10T aço inoxidável | 216 | 530 | 196 |
| Liga de aço inoxidável 304L | 241 | 586 | 193 |
| SA-508 Gr.3 Cl.2 (aço ferrítico de baixa liga) | 500 | 700 | 210 |
| 15Kh2NMFA (aço ferrítico de baixa liga) | 490 | 610 | 220 |
Rigidez de torção em diferentes formas geométricas
A forma geométrica de um objeto ou material também contribui para a sua rigidez à torção.
Secções transversais circulares
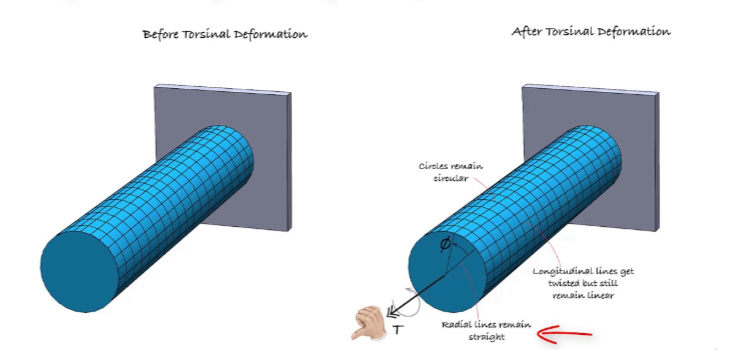
O material metálico circular resistirá ao binário a um nível elevado porque o material é distribuído uniformemente a partir do seu centro ou eixo de rotação, tornando-o mais resistente à torção.
Secções transversais rectangulares
As secções transversais rectangulares resistem à torção, mas não tanto como as secções transversais circulares. Isto deve-se ao facto de os materiais não estarem distribuídos uniformemente e de os lados não contribuírem muito para a rigidez do suporte.
Secções transversais ocas e complexas
As secções ocas, como tubos e canos, também suportam forças de torção a níveis elevados, porque a parte exterior do material trabalha para resistir à força, mantendo também pouco peso. São normalmente utilizadas em andaimes, vigas e veios de transmissão.
Rigidez de torção em diferentes materiais
Geralmente, os metais com um módulo de cisalhamento elevado resistem melhor ao binário do que a maioria dos polímeros ou compósitos, o que os torna adequados para aplicações que requerem uma elevada rigidez de torção.
PolímerosPor outro lado, têm um baixo módulo de cisalhamento e rigidez à torção. No entanto, também são úteis nalgumas operações, como o acoplamento flexível, em que é necessário algum nível de flexibilidade ou deformação.
Tabela de comparação de metais, polímeros e compósitos
| Tipo de material | Exemplo de material | Módulo de cisalhamento (G) em GPa | Momento de inércia polar (J)( ×10-6m4 | Rigidez de torção (GJ) Em Nm2 | Densidade relativa (kg/m³) | Aplicações comuns |
| Metal | Aço (AISI 1045) | 80 | 5 | 400 | 7050 | Vigas de veios de transmissão em pontes, engrenagens e veios de máquinas. |
| Metal | Alumínio (6061-T6) | 26 | 4 | 104 | 2700 | Estruturas de aeronaves, quadros de bicicletas, rodas de automóveis e braços. |
| Polímero | Polietileno (HDPE) | 0.8 | 3 | 2.4 | 950 | Tubos, uniões flexíveis, reservatórios, caixas de plástico. |
| Polímero | Policarbonato (PC) | 2.3 | 3.5 | 8.05 | 1200 | Equipamentos e capacetes de segurança, revestimento de aparelhos, vidros para automóveis |
| Compósito | CFRP | 100 | 6 | 600 | 1600 | Componentes aeroespaciais, automóveis de alto desempenho e equipamento desportivo |
| Compósito | CFRP | 25 | 4.5 | 112.5 | 1850 | Componentes marítimos, painéis para automóveis |
Como melhorar a rigidez à torção de um material
É possível melhorar a rigidez à torção de um material através das seguintes acções
Seleção do material adequado
Quanto mais elevado for o módulo de cisalhamento de um material, melhor será a sua rigidez de torção. O aço, por exemplo, tem um módulo de cisalhamento de 80GPa, o que o torna adequado para operações que exigem alta rigidez torcional.
No entanto, os polímeros têm um baixo módulo de cisalhamento de cerca de 0,5 a 3 GPa e, por conseguinte, não podem ser aplicados em casos em que é necessária rigidez à torção.
Aumentar o tamanho do objeto
Uma vez que as substâncias altamente densas suportam mais binário do que as de baixa densidade, é possível melhorar a rigidez de torção do objeto aumentando o seu tamanho. Desta forma, o objeto torna-se mais denso, aumentando a sua capacidade de resistir a forças de torção.
Melhorar o processo de produção
Anisotrópico Os materiais isotrópicos são conhecidos por terem diferentes níveis de rigidez de torção com base na direção da força de torção. Mantendo a uniformidade do material durante a produção e utilizando materiais isotrópicos, é possível melhorar o nível de rigidez de torção.
Aplicações da rigidez de torção na engenharia estrutural

Seguem-se algumas das aplicações da rigidez de torção na engenharia estrutural:
Arranha-céus e pontes
Com a aplicação da rigidez de torção, os engenheiros podem conceber pontes e arranha-céus capazes de suportar elevados níveis de força e cargas.
Podem determinar e construir estruturas capazes de resistir a forças naturais como os terramotos. Para evitar situações como o colapso de pontes ou edifícios, asseguram que todos os materiais estruturais criados estão em conformidade com o nível de rigidez necessário.
Vigas e colunas
As vigas e os pilares também precisam de ser criados para resistir a qualquer força ou carga de torção. São, por isso, concebidas para suportar componentes estruturais, incluindo coberturas, tectos, coberturas suspensas, etc., para evitar a torção causada por cargas, vento ou sismos.
Rigidez de torção em engenharia mecânica
Na engenharia mecânica, a rigidez torcional é vital, pois explica porque é que várias peças de máquinas, incluindo veios e engrenagens, mantêm um certo nível de rigidez quando sujeitas a uma força de torção.
Por exemplo, um veio só se dobra ligeiramente sob binário para que a ferramenta possa funcionar com precisão. Desta forma, evitam-se condições mecânicas adversas, mas melhora-se o desempenho.
Além disso, o funcionamento das engrenagens depende muito da rigidez de torção, uma vez que esta ajuda a erradicar os derrames, assegurando ao mesmo tempo a transmissão exacta da potência entre elas.
Do mesmo modo, na indústria automóvel e aeroespacial, a rigidez de torção ajuda a garantir a segurança e a melhorar o desempenho das peças de automóveis e aviões.
Conclusão
Para garantir a funcionalidade, eficiência e desempenho adequados dos componentes ou sistemas, é necessário garantir que o material mede o nível exato de rigidez de torção.
DEK responde a todas as suas necessidades em termos de materiais, garantindo que estes satisfazem o nível de rigidez à torção exigido pelo seu projeto. Quer necessite de orientação para a sua seleção de materiais metálicos ou deseje comprar alguns, estamos sempre disponíveis para discutir o assunto consigo. Não hesite em contactar-nos agora.
